Linear Programming
Problem 1 - Natural gas processing plant optimization
Problem Statement:
A natural gas processing plant can produce two grades of gas: Regular and Premium. The production of these grades of gas involve availability and time constraints shown in the table below - note that only one type of gas can be produced at a time.
| Resource | Regular | Premium | Total Available |
| Feed gas required | 7 m3/kg | 11 m3/kg | 77 m3/s |
| Production time | 10 h/kg | 8 h/kg | 80 |
| Max feed rate | 9 kg/s | 6 kg/s | |
| Profit | 150 cents/kg | 175 cents/kg |
Standard Form Representation:
Let X1 and X2 be the flow rates of Regular and Premium gas, respectively, in kg/s.
Let Z be the overall profit made by the processing plant.
Therefore, the task is to maximize the following objective function:
max Z(X_1, X_2 ) = 150X_1 + 175X_2
Such that:
7*X_1 + 11*X_2 ≤ 77 (Feed gas constraint)
10*X_1 + 8*X_2 ≤ 80 (Production time constraint)
0 ≤ X_1 ≤ 9 (Feed rate constraint 1)
0 ≤ X_2 ≤ 6 (Feed rate constraint 2)
X_1, X_2 ∈ Z+ (Optional positive integer value constraint)
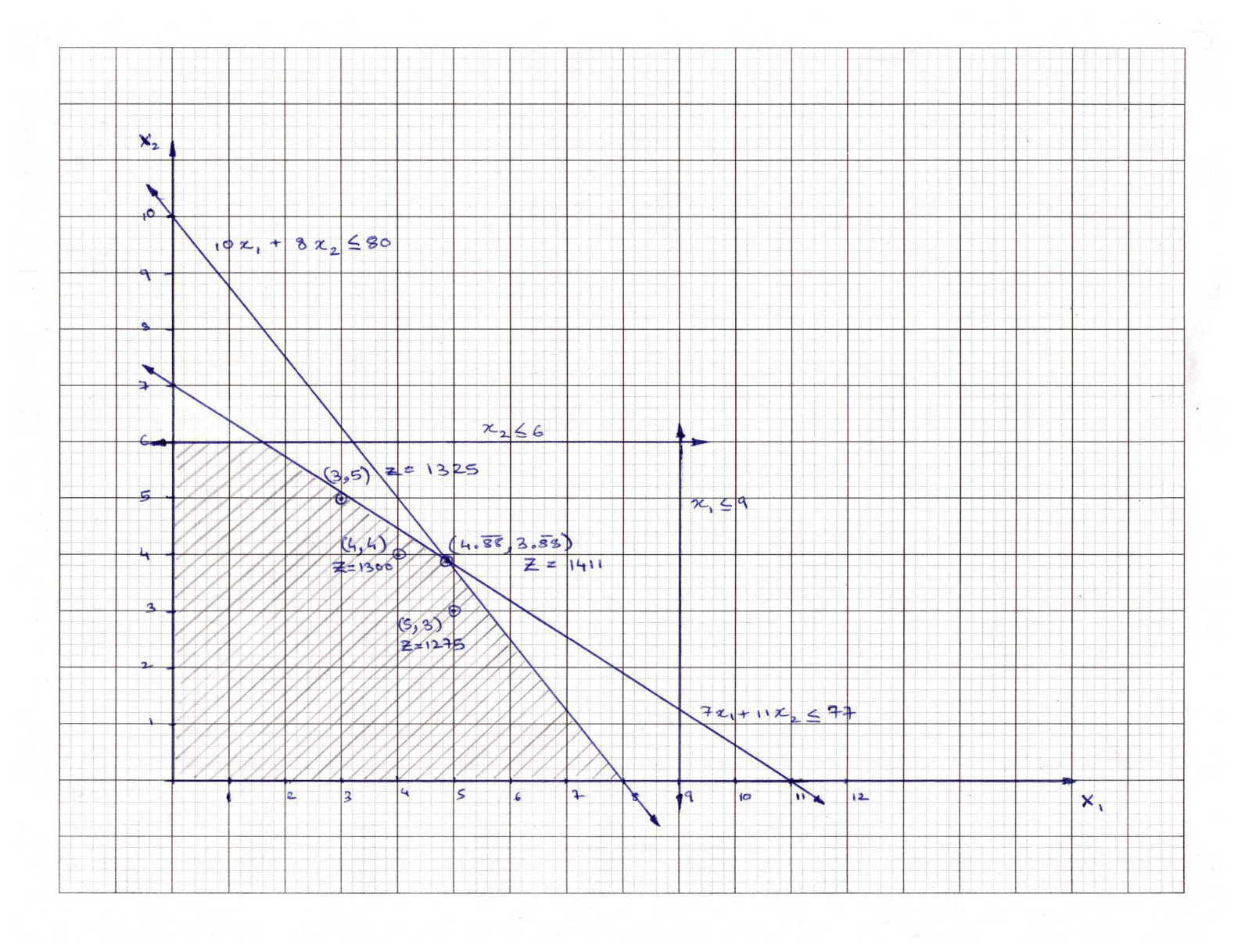
Linear Solution:
X_1 = 4.88, X_2 = 3.88, Z = 1411
Integer Solution:
X_1 = 3, X_2 = 5, Z = 1325
Solution Code: problem_1.m
Author: Yash Bansod
Date: 13th February, 2020
Problem 1 - Natural gas processing plant optimization
GitHub: https://github.com/YashBansod
Clear the environment and the command line
clear;
clc;
Define the optimization problem
% Define the objective function
f = [-150 -175];
% Constraint matrix and vector (A*X <= B)
A = [7 11; 10 8; 1 0; 0 1];
B = [77; 80; 9; 6];
Aeq = [];
beq = [];
lb = zeros(2, 1);
ub = inf(2, 1);
Find the solution
% Compute the solution using linear programming
[X, fval] = linprog(f, A, B, Aeq, beq, lb, ub);
% print out the solution obtained using linear programming
fprintf('Solution using linear programming: X1 = %f, X2 = %f\n', X)
fprintf('Profit: %f\n\n', -fval)
% Compute the solution using integer programming
[X, fval] = intlinprog(f, [1 2], A, B, Aeq, beq, lb, ub);
% print out the solution obtained using integer programming
fprintf('Solution using integer programming: X1 = %d, X2 = %d\n', X)
fprintf('Profit: %d\n\n', -fval)
Solution using linear programming: X1 = 4.888889, X2 = 3.888889 Profit: 1413.888889
Solution using integer programming: X1 = 3.000000e+00, X2 = 5.000000e+00 Profit: 1325
Problem 2 - Automobile Shop Optimization
You own of a shop producing automobile trailers and wish to determine the best mix for your three products: flat-bed trailers, economy trailers and luxury trailers. The shop is limited to working 24 days/month on metalworking and 60 days/month on woodworking for these products. This table indicates production data for trailers.
| Usage per unit of trailer | Resources | |||
| Flat-Bed | Economy | Luxury | ||
| Metalworking | 0.5 | 2 | 1 | 24 |
| Woodworking | 1 | 2 | 4 | 60 |
| Value/Profit ($ x 100) | 6 | 14 | 13 | |
Standard Form Representation:
Let X1, X2, and X3 be the number of units to be produced of flat-bed trailers, economy trailers and luxury trailers respectively.
Let Z be the overall profit made by the production shop (as multiple of $100).
Therefore, the task is to maximize the following objective function:
max Z(X_1, X_2,X_3 ) = 6*X_1 + 14*X_2 + 13*X_3
Such that:
0.5*X_1 + 2*X_2 + X_3 ≤ 24 (Metalworking constraint)
X_1 + 2*X_2 + 4*X_3 ≤ 60 (Woodworking constraint)
X_1, X_2, X_3 ∈ R+ (Positive real value constraint)
X_1, X_2, X_3 ∈ Z+ (Optional positive integer value constraint)
Linear Solution:
X_1 = 36, X_2 = 0, X_3 = 6, Z = 294
Integer Solution:
X_1 = 36, X_2 = 0, X_3 = 6, Z = 294
Solution Code: problem_2a.m
Author: Yash Bansod
Date: 13th February, 2020
Problem 2a - Automobile Shop Optimization
GitHub: https://github.com/YashBansod
Clear the environment and the command line
clear;
clc;
Define the optimization problem
% Define the objective function
f = [-6 -14 -13];
% Constraint matrix and vector (A*X <= B)
A = [0.5 2 1; 1 2 4];
B = [24; 60];
Aeq = [];
beq = [];
lb = zeros(3, 1);
ub = inf(3, 1);
Find the solution
% Compute the solution using linear programming
[X, fval] = linprog(f, A, B, Aeq, beq, lb, ub);
% print out the solution obtained using linear programming
sprintf('Solution using linear programming: X1 = %f, X2 = %f, X3 = %f', X)
sprintf('Profit: %f', -fval)
% Compute the solution using integer programming
[X, fval] = intlinprog(f, [1 2 3], A, B, Aeq, beq, lb, ub);
% print out the solution obtained using integer programming
sprintf('Solution using integer programming: X1 = %d, X2 = %d, X3 = %d', X)
sprintf('Profit: %d', -fval)
Solution using linear programming: X1 = 36.000000, X2 = 0.000000, X3 = 6.000000 Profit: 294.000000
Solution using integer programming: X1 = 36, X2 = 0, X3 = 6.000000e+00 Profit: 294
Dual of Standard Form:
Let Y1 and Y2 be the value (shadow price) of metalworking and woodworking resources.
Let W be the minimum acceptable price for the resources (as multiple of $100).
min W(Y_1, Y_2) = 24*Y_1 + 60*Y_2
Such that:
0.5Y_1+Y_2≥6 or -0.5Y_1-Y_2≤6 (Resource value for flat-bed trailers)
2*Y_1 + 2*Y_2 ≥ 14 or -2*Y_1 - 2*Y_2 ≤ 14 (Resource value for economy trailers)
Y_1 + 4*Y_2 ≥ 13 or -Y_1 - 4*Y_2 ≤ 13 (Resource value for luxury trailers)
Y_1, Y_2 ∈ R+ (Positive real value constraint)
Linear Solution:
Y_1 = 11, Y_2 = 0.5, Z = 294
Solution Code: problem_2b.m
Author: Yash Bansod
Date: 13th February, 2020
Problem 2b - Automobile Shop Optimization (Dual)
GitHub: https://github.com/YashBansod
Clear the environment and the command line
clear;
clc;
Define the optimization problem
% Define the objective function
f = [24 60];
% Constraint matrix and vector (A*Y <= B)
A = [-0.5 -1; -2 -2; -1 -4];
B = [-6; -14; -13];
Aeq = [];
beq = [];
lb = zeros(2, 1);
ub = inf(2, 1);
Find the solution
% Compute the solution using linear programming
[Y, fval] = linprog(f, A, B, Aeq, beq, lb, ub);
% print out the solution obtained using linear programming
sprintf('Solution using linear programming: Y1 = %f, Y2 = %f', Y)
sprintf('Minimum acceptable price: %f', fval)
Solution using linear programming: Y1 = 11.000000, Y2 = 0.500000 Minimum acceptable price: 294.000000